Map of propagation risk of COVID-19 by local contact in Spain
Motivation
The spread of COVID-19 is posing many challenges to our social and health systems. One of them is predicting and quantifying the emergence of new cases that follow local contagion at a national scale. By local contagion we refer to those cases of individuals that are infected with the virus but for which the source of infection is unknown, that is, the person affected has not reported any travel to affected areas or any direct contacts with other infected individuals.
One of the major difficulties we are currently facing is the early detection of cases, which is essential for its confinement and medical treatment. A crucial feature of this virus is that it presents an asymptomatic phase, where the infected individual is infectious but presents mild or no symptoms. This period is considerably long, and can last up to 14 days according to the present reported data. The current lack of measures to detect infection cases in their early stages in addition to the existence of this asymptomatic phase influences to a large extent the spreading of the epidemics and the implementation of effective control measures.
In this website we show the results of the estimated epidemic risk in Spain, at a municipal level, as obtained by a model of epidemic spreading which takes into account the recurrent mobility patterns (commuting) among municipalities. This data has been provided by the Instituto Nacional de Estadística (INE) (National Institute of Statistics) of Spain.
Our model currently includes the epidemiological data reported up to the present moment for the virus responsible of the COVID-19 (now officially named SARS-CoV-2) and demographical and mobility data for each municipality in Spain. This model can also be directly applied to other countries and regions for which such mobility and demographics data is available.
Results
Risk map
The risk map generated with our model produces an indicator for each municipality of the fraction of the population that is estimated to have contracted the infection of SARS-CoV-2 through local contact. Those areas shaded in gray correspond to areas for which there is no data available.
The numerical data corresponding to the map can be downloaded here in Excel format and here in pdf format.
Hospital overload map
After estimating, using our model, the number of expected infections of COVID-19, we can calculate the overload that the health care facilities in Spain will face in attending patients requiring ICU attention.
Our assumptions are the following. First, we are assuming the most optimistic scenario regarding the occupation of the ICU units, which is 0% before COVID-19, meaning we assume all ICU units are available for COVID patients. Under this scenario we calculate the total number of infections that will require ICU hospitalization for the day of 18 of March. This value is calculated as the 5% of the total number of cases that our model predicts for that day. This 5% corresponds to the number of cases of COVID-19 that required ICU in Spain, as published in the most recent official reports.
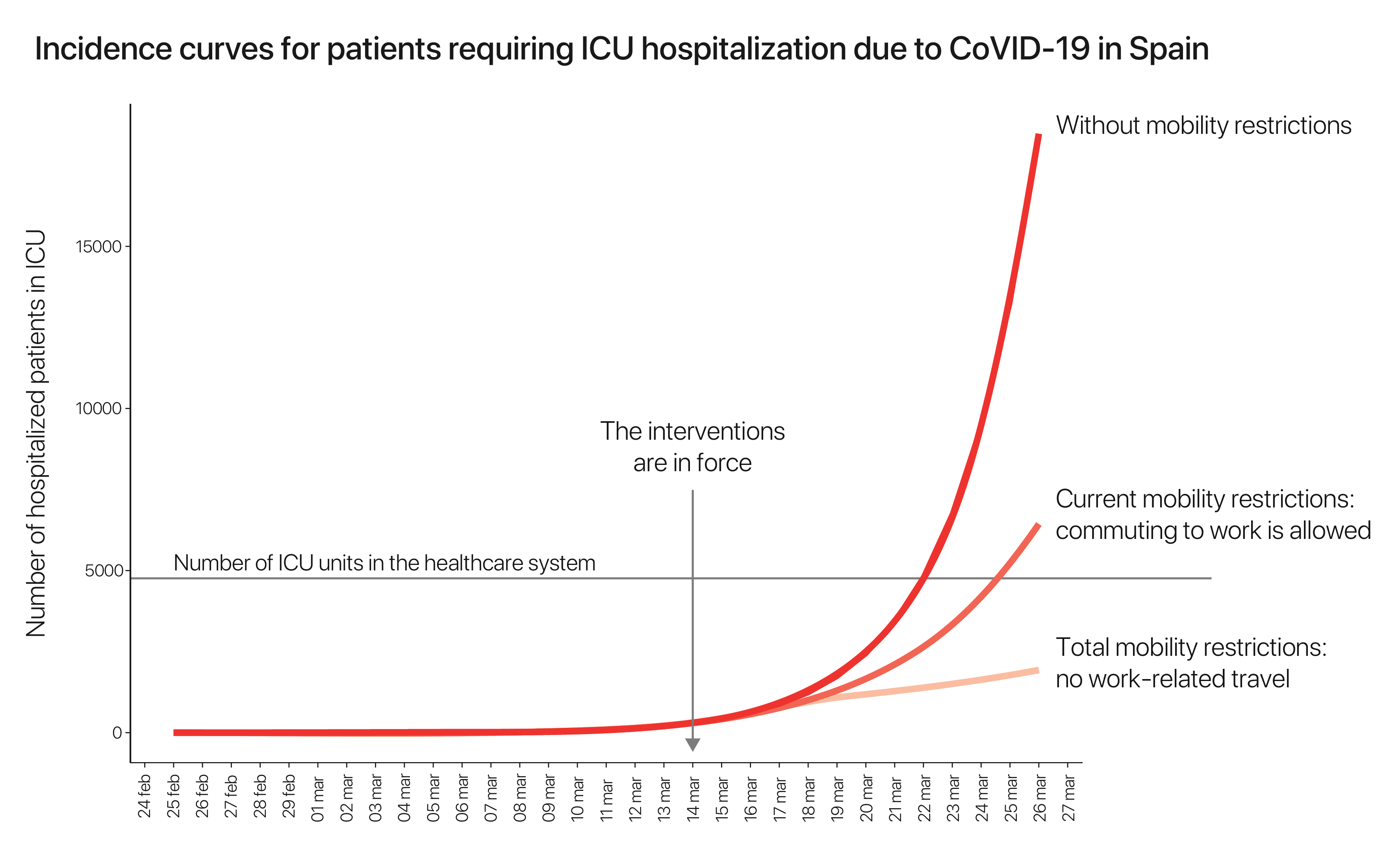
Incidence curves for patients requiring ICU hospitalization due to COVID-19 in Spain
In the following we present the evolution of the number of patients that will require ICU hospitalization due to COVID-19. The curves are calculated using our model, for three different types of interventions:
- With no mobility restrictions.
- With partial mobility restrictions: commuting to work is allowed in a 50%.
- With total restrictions of mobility: work-related traveling is not allowed except for basic services.
We observe how the different interventions have different outcomes in terms of overloading the ICU healthcare facilities.
Model
A mathematical model for the spatiotemporal epidemic spreading of COVID19
medRxiv 2020.03.21.20040022
The full description of the model is available for download here .
The model we are using is a new version of a family of epidemiological models in discrete time, that has been specifically modified to represent the particular spreading dynamics of SARS-COV-2, the virus causing COVID-19.
The objective of the model is to estimate the risk for every municipality in Spain, taking into account the following factors: (I) The dynamics of the transmission of SARS-COV-2, and (II) the recurrent mobility flows in Spain, and (III) the demography of the Spanish population.
With respect to modeling the transmission of the virus, we use a compartmental model, meaning that we divide the population according to their infection status. These compartments are:
- Susceptible: an individual that has not been infected yet but is susceptible to infection.
- Exposed: an individual who is infected but not yet infectious, because he/she still is in an incubation phase.
- Asymptomatic (or displaying mild symptoms): an individual who is infected and infectious, but does not show clear symptoms of COVID-19.
- Infected: in our model, an infected individual is infectious and does show clear symptoms compatible with COVID-19, making its detection easier than those in the Asymptomatic compartment.
- Hospitalized: an infected individual that has been detected and that requires hospitalization. This individual is not considered to be infectious anymore as it is supposed to be confined inside the hospital.
- Recovered/removed: an individual who has been infected at a moment in time, but who in the current moment, is not infectious anymore. This could happen because the individual has recovered from the infection and developed immunity, or because the patient has died.
The transitions among the previous compartments are regulated with the specific parameters of the model (transmission probability, recovery probability...etc), and have been derived from the scientific literature published up to the present moment.
Regarding mobility, we have used data made available by the Instituto Nacional de Estadística (INE, Spain), that record those mobility flows inside and among municipalities that are observed recurrently, because of habitual commuting to and from the workplace. This data set reports only those flows that involve more than 10 trips, and for municipalities larger than 100 inhabitants. We incorporate the commuting mobility in our model because we deem it fundamental to understand how the infection spreads through the territory. Our model can also be used to simulate certain mobility restrictions (either local or global), and calculate the resulting risk estimates that we would observe under such restrictions.
With respect to the demography, we have considered essential to divide the population of the country in three compartments: young people (from 0 to 25 y.o.), adults (26-65) and elderly (>66). Very recent evidence reports that COVID-19 affects very differently each of these age compartments. In our model, the differences that we establish between the three groups are, essentially:
- Young people and elderly do not travel across the territory with the same probability as adults do.
- Young people have, with more probability than the other two compartments, infections where only an asymptomatic (or with mild symptoms) phase is observed, making these infections harder to detect.
- Elderly people go to the hospitalized compartment with a much higher probability than young people or adults.
Limitations
- The model does not predict the imported international cases (those individuals that have been infected outside the country and then traveled to Spain).
- The model is working with epidemiological parameters as reported up to the present moment in the medical and scientific literature, but can be changed upon new discoveries.
- The model assumes that the mobility data as reported by INE do not change. Our estimation would substantially differ if mobility restrictions were imposed.
Advantages
- The model allows altering the epidemiological parameters as soon as new epidemiological studies report them.
- The model allows to study the influence of the asymptomatic period and its associated infectivity.
- Taking into account the epidemiological factors and the mobility and demography data, we can estimate the map of risk of new cases, which allows us to anticipate the spreading of the virus through asymptomatic individuals.
- Massive restriction mobility (quarantine policies) can easily be introduced in the model, allowing us to obtain a new estimate of the risk under these new measures. This would allow policy makers and authorities to obtain an estimation of the efficacy of such measures.
The problem with the data
Our model can calculate, starting from a set of initial conditions (i.e. a certain number of detected cases and their exact location), an estimation of how would the epidemic evolve in Spain. In the first phase of the spreading of SARS-COV-2 in Spain, the majority of the reported cases were “imported”, that is, individuals that had traveled to other infected countries, got infected there and then traveled to Spain. These cases cannot be detected by our model because they are external to the transmission dynamics of the virus inside the country. For that reason, in a phase where the imported cases conform the majority of the detected positives in the country, it is crucial to have accurate, reliable data to be able to calculate our estimates. Given that it proved impossible to have access to such data, we decided to temporarily discontinue the updating of our risk map.
In the present moment, however, a great number of detected infection cases in Spain are already “native”, meaning that they have been originated inside the country, by local transmission. These kind of cases are well detected by our model, which, starting out from the initial conditions of the first phase of the epidemics (where the vast majority of the cases were imported), is able to make the system evolve and produce the infection risk estimate. For this reason we are in the position of offering new results through our risk map.
Frequently Asked Questions
In this map we plot, for each municipality in Spain, an indicator of the fraction of the population that we estimate might have been infected by COVID-19 by local contact.
A mathematical model is a simplified abstraction of reality in the form of mathematical equations. The equations obtained can be used to understand what phenomena would we observe under certain conditions. The most common example of a mathematical model are meteorology models, used for weather forecasting.
Our model is a new version of a family of models already established in the scientific literature, called compartmental epidemiological models. In this particular model, which has been especially designed for the spreading of COVID-19, we assume that an individual might be in a susceptible state, in the exposed state (infected but not yet infectious), in an infectious asymptomatic state, in an infectious and symptomatic state, or in a recovered or removed state. The transitions between the previous compartments are regulated by the specific parameters for this disease.
The parameters have been obtained from the most recent scientific literature about the epidemiological traits of this new virus causing the disease COVID-19 (now officially termed SARS-CoV-2). The parameters could be modified depending on the results of the ongoing research.
No. A risk indicator of a 0.1% in a municipality means that we estimate that 1 of every 1000 individuals of that municipality might be infected (either in a symptomatic or asymptomatic state). The probability of contracting the disease depends on more factors, like for instance, the number of contacts that one individual makes, the infectivity of the disease, etc. The risk of infection of each municipality that we plot on the map could be interpreted as the “potential health state with respect to COVID-19 of that municipality".
No. That is the process we followed during the first days of infection in Spain, because most of the detected cases were “imported”, and therefore they had to be introduced in the model by hand. At the present moment, the spreading of the epidemic is in another phase, where most of the infection cases are result of local contagion. These local infections are well captured by our model, meaning our model is able to reproduce them. We are now feeding our model with the initial conditions of the first phase of the epidemics (the number of reported cases in that phase), we let the model evolve and we plot the risk estimate prediction for the following days.
The key is the fact that the epidemic is now in a different phase. At the very beginning, there were very few reported cases and most of them were imported (i.e. exogenous to our model). In such a scenario, the model was very sensitive to the initial conditions (the number and exact location of the identified contagions). For this reason, it was necessary to update the initial conditions as new cases were reported, and the forecast obtained was only valid at a very short term. Now that the epidemic has evolved into a second phase mostly characterized by local contagions, we can evaluate the model for more timesteps and obtain the risk estimate for several days.
We are using the mobility data from the Instituto Nacional de Estadística, which accounts for the mobility of the population who works in each municipality. This data reports, principally, the home-to-work mobility and viceversa, although they contain other mobility factors not necessarily work-related.
This means that there is no available mobility data for that municipality, most likely because its population falls below 100 inhabitants.
The mobility data that is at our disposal only reports those flows of daily recurrent mobility that comprise more than 10 individuals. In the case of areas where there is a 0% risk reported even if they are surrounded by areas with positive risk, what happens is that the ingoing and outgoing flows to and from that region are not reported, and to all effects, it behaves like an isolated area.
Authors
Coordinadores del proyecto
Alex Arenas (Universitat Rovira i Virgili, Tarragona, Spain)
Jesús Gómez-Gardeñes (Universidad de Zaragoza, Zaragoza, Spain)
Investigadores participantes
Wesley Cota (Universidade Federal de Viçosa, Minas Gerais, Brazil)
Sergio Gómez (Universitat Rovira i Virgili, Tarragona, Spain)
Clara Granell (Universidad de Zaragoza, Zaragoza, Spain)
Joan T. Matamalas (Harvard Medical School, Boston, USA)
David Soriano-Paños (Universidad de Zaragoza, Zaragoza, Spain)
Benjamin Steinegger (Universitat Rovira i Virgili, Tarragona, Spain)
Colaborators
Portugal Section
Nuno Araújo (Centro de Física Teórica e Computacional, Faculdade de Ciências, U Lisboa, Portugal)
Hygor Piaget Melo (Centro de Física Teórica e Computacional, Faculdade de Ciências, U Lisboa, Portugal)
Partners: NOS, Data Science Portuguese Association, and Closer Consulting
Brazil Section
Wesley Cota (Universidade Federal de Viçosa, Minas Gerais, Brazil)
Silvio C. Ferreira (Universidade Federal de Viçosa, Minas Gerais, Brazil)